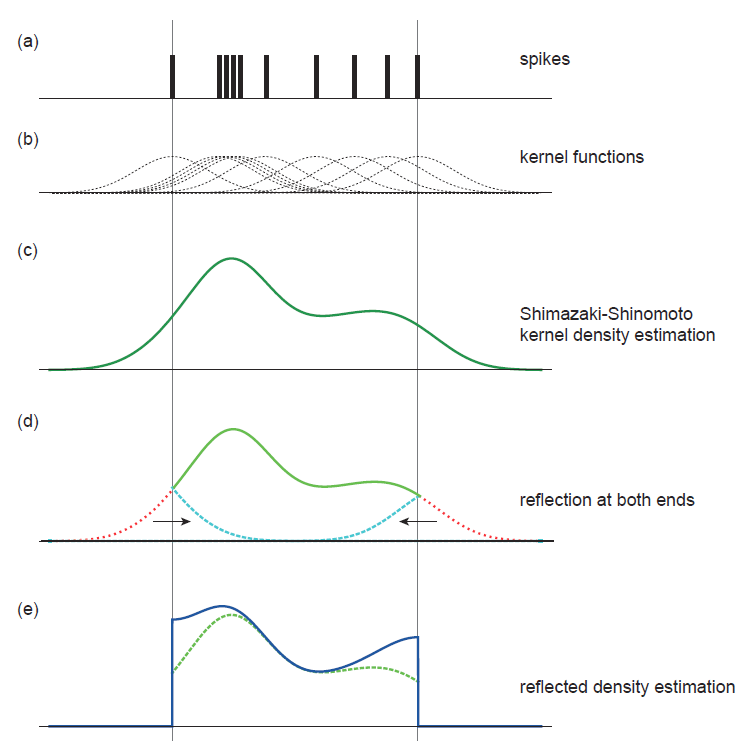
Fig.1 Composing the reflected kernel density estimation. (a) Spike times. (b) Kernel functions for spikes. (c) Kernel density estimation. (d) Reflecting the leakage density. (e) Reflected density estimation.
| The method of optimizing kernel density estimate was rigorously derived
under the principle of minimizing the mean integrated squared error between
the density estimation and the unknown underlying rate [1]-[3]. For a practical time series analysis, however, there may be a loss at the boundaries; the rate estimation at both ends may drop because the kernel density leaks out (Fig. 1c). Here we suggest compensating the leak by folding back the leakage density at each end (Fig.1d) and by adding it to the original density (Fig.1e). Accordingly, the loss at both ends is recovered. |
| Fig.1 Composing the reflected kernel density estimation. (a) Spike times. (b) Kernel functions for spikes. (c) Kernel density estimation. (d) Reflecting the leakage density. (e) Reflected density estimation. |
[1] Shimazaki H and Shinomoto S (2010) Kernel bandwidth optimization in spike
rate estimation. J. Computational Neuroscience 29:171-182.
[2] Web application for the kernel smoother
[3] Comprehensive application programs.
|
I. Let 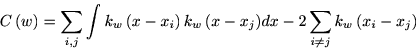 III.Find The present algorithm speeds up the computation by neglecting the unnecessary parts outside the range of ± 5 w of the Gaussian kernel in the double summation II (see Shinomoto S., Estimating the firing rate. in Analysis of Parallel Spike Train Data. eds. S. Gruen and S. Rotter, (Springer, New York, 2010)). |
If you have any questions, or have suggestions for improving the programs, please contact Shigeru Shinomoto, who is conducting these studies.
be your data. Let the kernel with bandwidth 
be 
.
that minimizes 